In-Depth Analysis of Cleaning Times Using the Weibull Distribution
Understanding and predicting cleaning times is essential for efficient resource management and operational planning. This article is about the application of the Weibull distribution for analyzing cleaning times, particularly focusing on predicting the maximum time needed to clean multiple accommodations with a high level of confidence.
Introduction
Cleaning times for accommodations can vary significantly due to various factors such as room size, condition, and cleaning crew efficiency. To manage these variations and improve efficiency, we can use statistical tools to model and predict cleaning times. The Weibull distribution is particularly well-suited for this purpose due to its flexibility in modeling different types of data distributions.
The Weibull Distribution
The Weibull distribution is widely used in reliability engineering and life data analysis. It is defined by two parameters: the scale parameter (λ) and the shape parameter (k).
The shape parameter defines the form of the data’s distribution, often called the Weibull slope by statisticians because it corresponds to the slope of the line on a Weibull probability plot. For example, a shape parameter of 2 produces a Rayleigh distribution, which is equivalent to a Chi-square distribution with two degrees of freedom. A shape parameter close to 3 approximates the normal distribution.(*)
The scale parameter indicates the distribution’s spread or variability. Specifically, the scale parameter is the value below which 63.2% of the distribution’s data points fall, representing the 63.2nd percentile.(*)
Probability density function
The probability density function (PDF) of the Weibull distribution is given by:
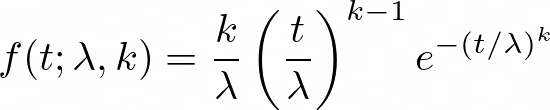
where t is the time, λ is the scale parameter, and k is the shape parameter. The cumulative distribution function (CDF) is:
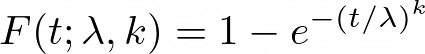
The shape parameter k determines the form of the distribution:
– If k < 1, the distribution is decreasing, indicating that most cleaning times are short.
– If k = 1, the distribution is exponential, indicating a constant rate of cleaning times.
– If k > 1, the distribution initially increases and then decreases, indicating a peak in cleaning times.
The scale parameter λ affects the spread of the distribution. A higher λ value indicates more variability in cleaning times.
Data Collection and Analysis
Collecting Data
To analyze cleaning times, we first collected actual cleaning duration data from various accommodations in a certain amount of time (n=113) in the summer of 2021. The dataset included cleaning times in minutes.
Fitting the Weibull Distribution
Using the Python library SciPy, we fitted the Weibull distribution to our data. The function `stats.weibull_min.fit` was employed for this purpose, which uses maximum likelihood estimation (MLE) to find the best-fitting parameters.
Here is a sample code snippet for fitting the Weibull distribution:
import numpy as np
from scipy.stats import weibull_min
# Sample data: cleaning times in minutes
data = [30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90]
# Fit Weibull distribution to data
shape, loc, scale = weibull_min.fit(data, floc=0)
print(f"Shape parameter (k): {shape}")
print(f"Scale parameter (λ): {scale}")
From the collected data, we obtained a shape parameter k of 1.92 and a scale parameter λ of 34. With the Weibull parameters in hand, we can make informed predictions about cleaning times.
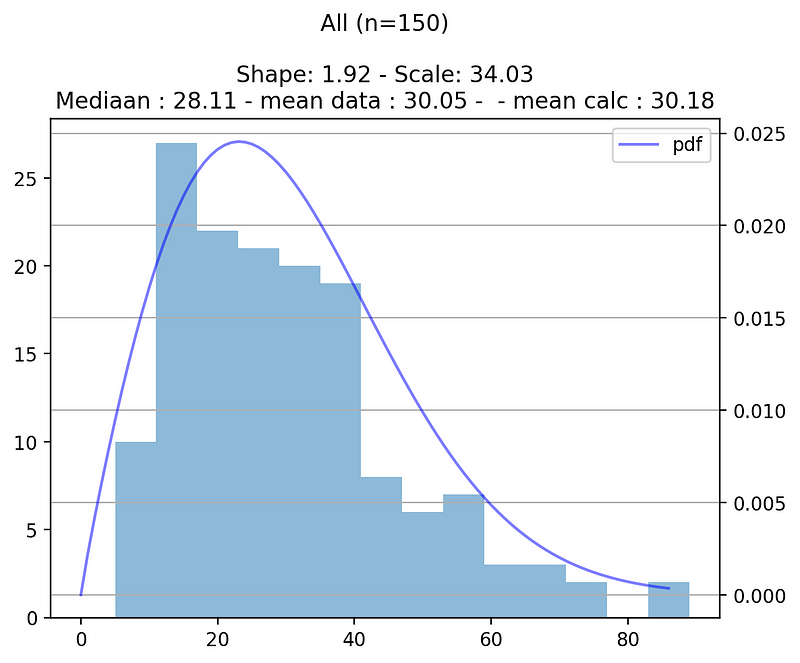
Case study : cleaning 10 accommodations
As an example from the real world, we aim to determine the maximum time required to clean 10 accommodations with a 95% confidence level, meaning there is only a 5% chance that the total cleaning time will exceed this value.
Step-by-Step Calculation
Calculating the 95th Percentile for One Accommodation
First, we calculate the 95th percentile for cleaning a single accommodation. This involves solving the CDF equation for t when F(t; λ, k) = 0.95 :
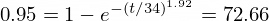
With Python we calculate with this code
import numpy as np
# Given Weibull parameters
k = 1.92
lambda_ = 34
# 95th percentile calculation for one accommodation
p = 0.95
t_95_one = lambda_ * (-np.log(1 - p))**(1/k)
print(t_95_one)
The 95th percentile for cleaning a single accommodation is approximately 72.66 minutes.
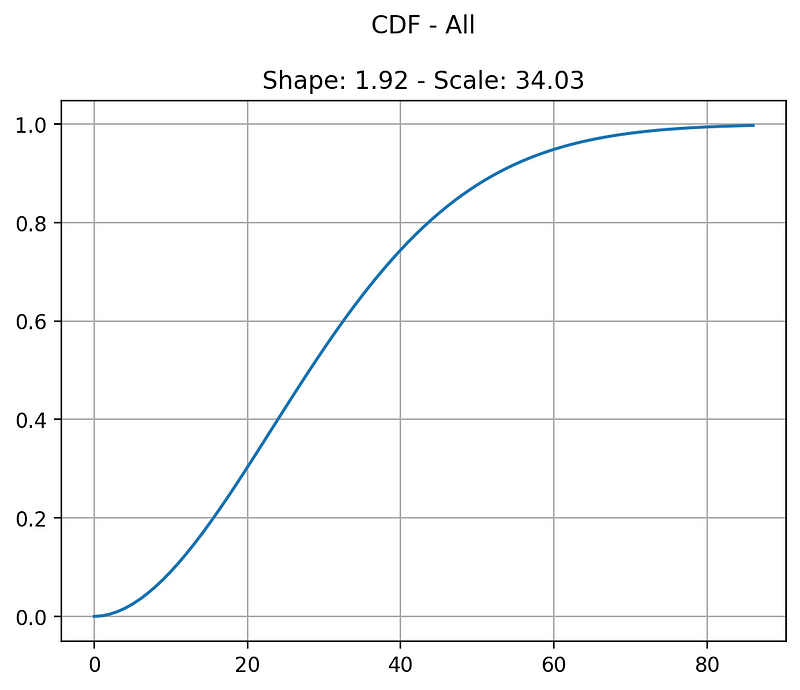
Extending to 10 Accommodations
To find the maximum time for cleaning 10 accommodations, we consider the sum of 10 independent Weibull-distributed random variables. Due to the Central Limit Theorem, the distribution of this sum can be approximated by a normal distribution.
Mean and Standard Deviation
For a single Weibull distribution, the mean (μ) and variance (σ²) are given by:
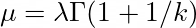
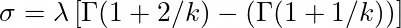
For 10 accommodations, the mean is 10 times the mean for one, and the standard deviation is √10 times the standard deviation for one.
Using Python to compute these:
import scipy.stats as stats
# Given Weibull parameters
k = 1.92
lambda_ = 34
# Mean and standard deviation for one Weibull distribution
mean_time = lambda_ * np.gamma(1 + 1/k)
std_time = np.sqrt(lambda_**2 * (np.gamma(1 + 2/k) - (np.gamma(1 + 1/k))**2))
# Parameters for the sum of 10 independent Weibull distributions
mean_sum = 10 * mean_time
std_sum = np.sqrt(10) * std_time
# Find the 95th percentile for the total time
total_time_95 = stats.norm.ppf(0.95, loc=mean_sum, scale=std_sum)
print(total_time_95)
The 95th percentile total cleaning time for 10 accommodations is approximately 469 minutes. This means there is only a 5% chance that the total cleaning time for 10 accommodations will exceed 469 minutes.
Conclusion
By applying the Weibull distribution to our cleaning time data, we can make accurate predictions about the maximum time required for cleaning multiple accommodations. This analysis, which incorporates advanced statistical methods, reveals that with 95% confidence, the total cleaning time for 10 accommodations will not exceed 469 minutes (7.8 hours). This information is crucial for optimizing cleaning schedules, resource allocation, and improving overall operational efficiency.
Sources
- https://statisticsbyjim.com/probability/weibull-distribution/
- Wikipedia contributors. (2023, June 18). Weibull distribution. In Wikipedia, The Free Encyclopedia. Retrieved from https://en.wikipedia.org/wiki/Weibull_distribution
- Interactive graphs
https://rcsmit-streamlit-scripts-menu-streamlit-fiaxhp.streamlit.app/?choice=5 - Source code
https://github.com/rcsmit/streamlit_scripts/blob/main/schoonmaaktijden.py - Data
https://docs.google.com/spreadsheets/d/1Lqddg3Rsq0jhFgL5U-HwvDdo0473QBZtjbAp9ol8kcg/edit?gid=0#gid=0 - Gerhards, C., Schramm, M., & Schmid, A. (2019). Use of the Weibull distribution function for describing cleaning kinetics of high pressure water jets in food industry. Journal of Food Engineering. doi:10.1016/j.jfoodeng.2019.02.011
