Hoe het RIVM de verwachte sterfte berekent

Magic black box of zuivere wiskunde?

Elk jaar in juli publiceert het RIVM de verwachte sterfte. Dit jaar valt die lager uit dan verwacht, terwijl de werkelijke sterfte juist stijgt. Dat roept vragen op: hoe werkt dit algoritme eigenlijk? Wordt het aangepast wegens een bepaald agenda?

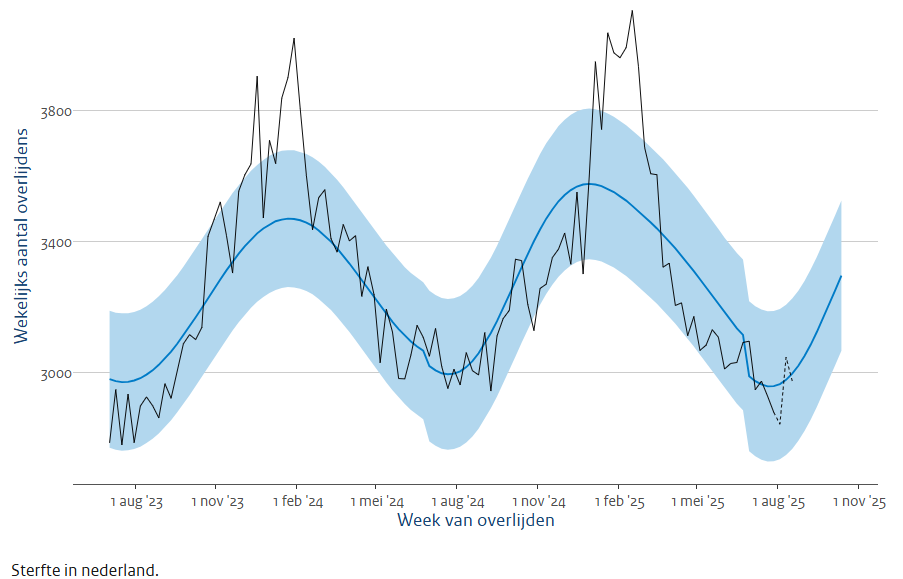
Ik heb al eerder over deze verwachtingen geschreven en het script gereproduceerd. De resultaten hiervan sloten ook goed aan bij de van het RIVM. Helaas liet mijn code 2025/206 niet zien en het was zo’n spaghetti dat ik met hulp van ChatGPT en Grok mijn eerdere code heb herschreven.

In deze blogpost probeer ik uit de methode van het RIVM uit te leggen.

Hoe werkt OLS?

Het werkt met lineaire regressie. Dit is het model dat een lijn zoekt door de data. De rekenmethode heet OLS die bepaalt welke lijn het best past door de gevonden waardes.

De iets versimpelde formule is :

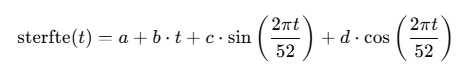
Hieronder zie je de grafiek als a=1, b=0, c=10 en d=10

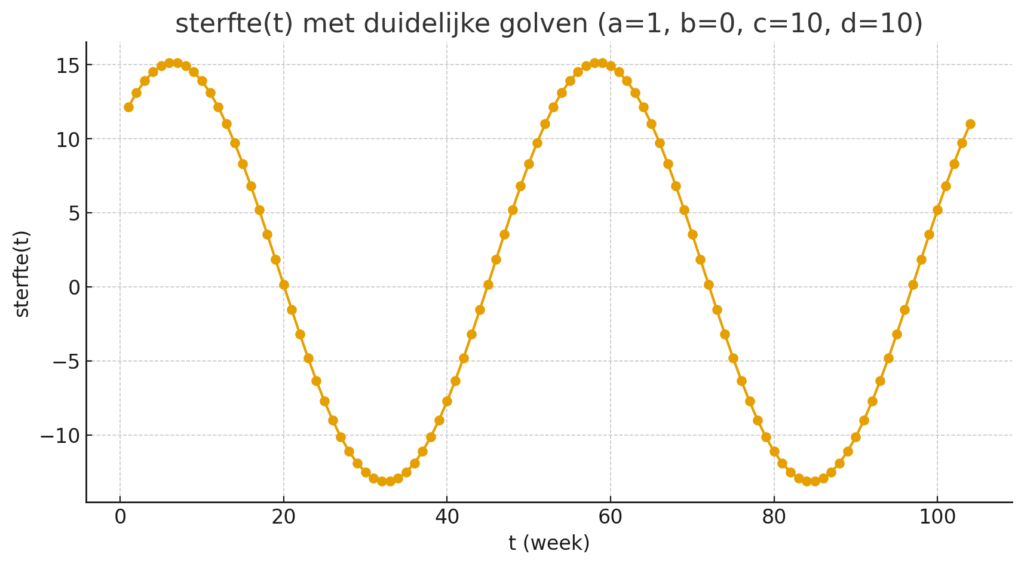
We proberen de waardes van a,b,c en d zo te vinden dat de gevonden lijn het minste afwijkt van het aantal overledenen.

Het algoritme stap voor stap

We gaan het aantal overledenen voorspellen in 2020 tot en met 2025 (NB: we werken van juli tot en met juni. Als we 2020 zeggen, bedoelen we juli 2019 tot en met juni 2020)

We beginnnen met 2020, wat ik het doeljaar noem. Hiervoor kijken we naar de waardes van 2015,2016,2017, 2018 en 2018. Dit noem ik het referentiekader

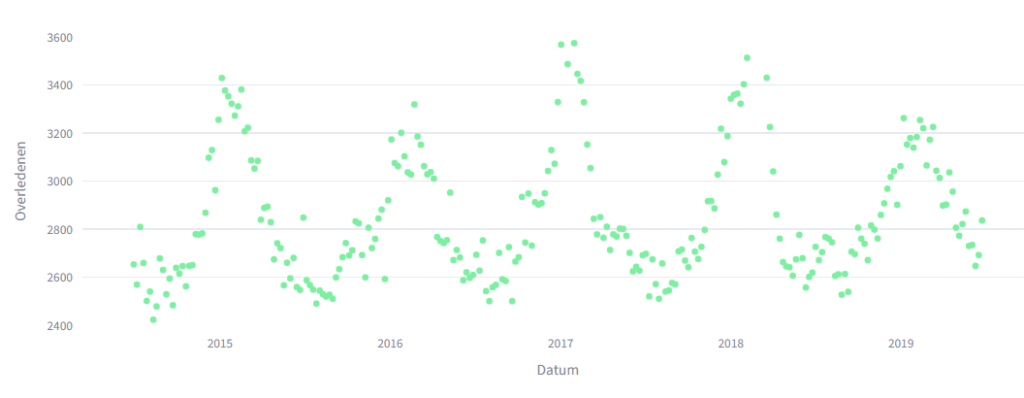
Om de vertekening van seizoenssterfte (griep in te winter en hittedoden in de zomer) weg te halen, tellen we pieken niet mee en filteren ze de 25% hoogste waardes in het referentiekader en de 20% hoogste waardes in juli en augustus weg. We houden dan deze waardes over.

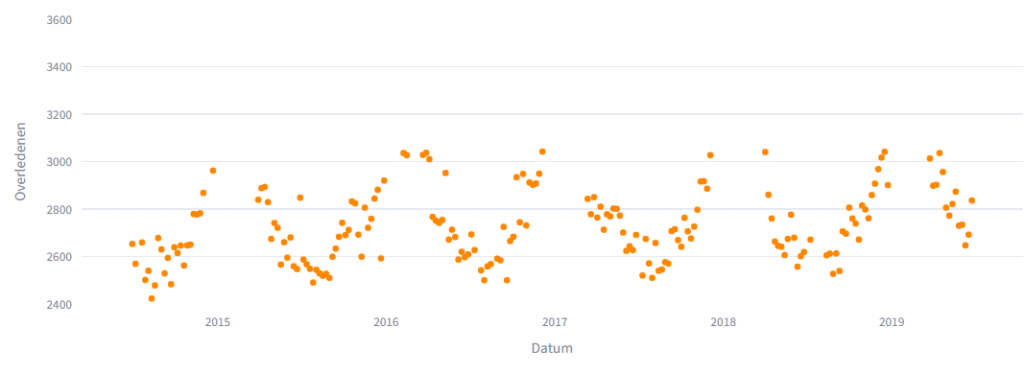
Dit lijkt op een mooie golfbeweging. Als ik de hierboven beschreven OLS toepas, weet ik de waardes van a,b,c en d.

Als ik die invul in de formule en teken in de grafiek, krijg ik dit.

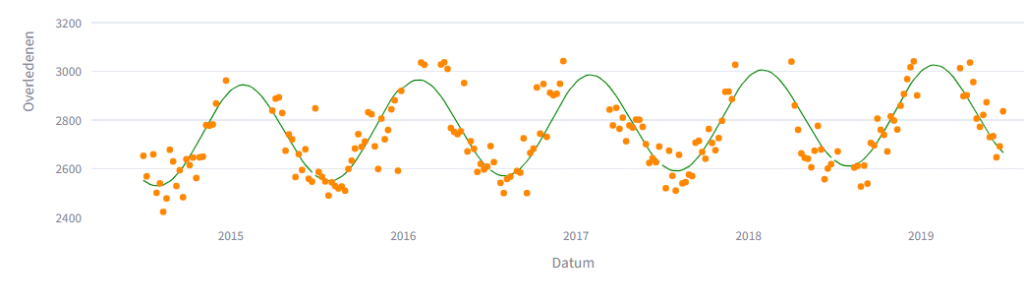
Het mooie is dat ik de waardes van a tot en met d ook kan invullen voor 2020, mijn doeljaar.

Dit stukje zet ik op een apart resultaatpapiertje

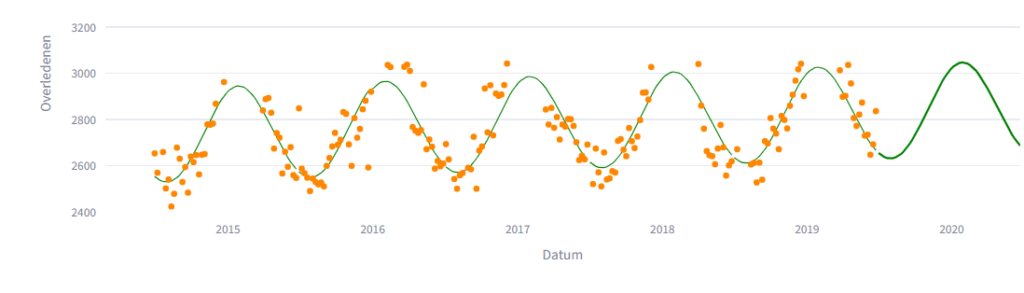
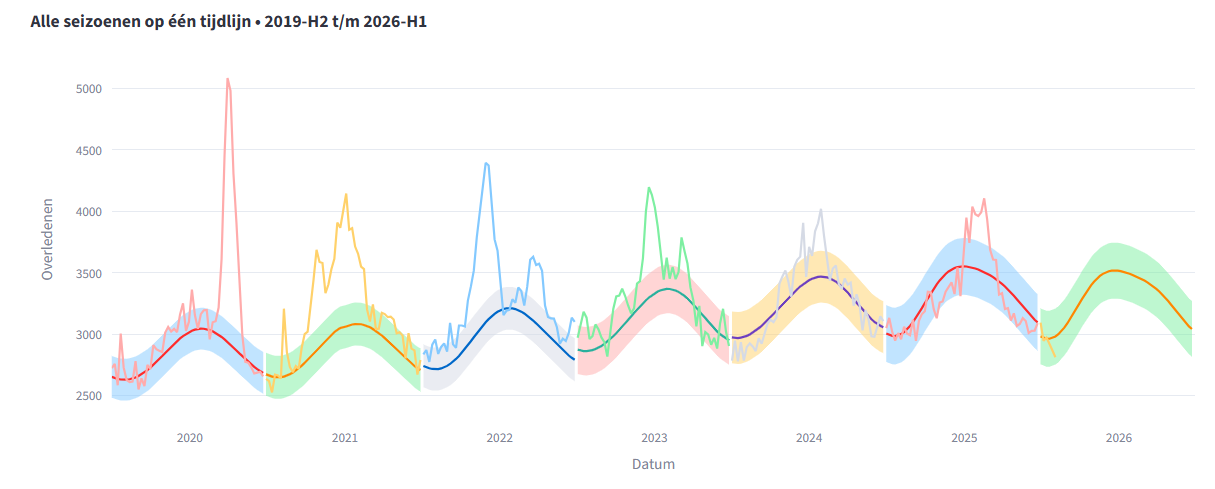
Alle jaren bij elkaar brengen

Nu ga ik het referentiekader en doeljaar een jaar naar rechts schuiven. Het doeljaar wordt 2021 en het nieuwe referentiekader is 2016 tot en met 2020.

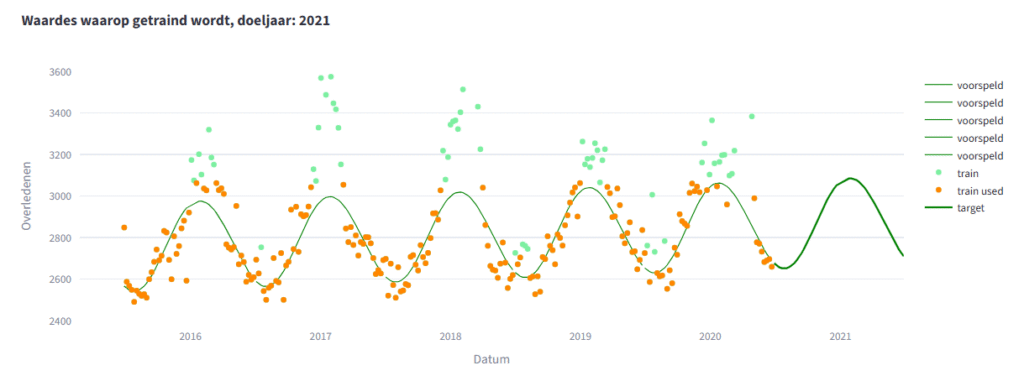
Nu ga ik alle resultaatpapiertjes naast elkaar leggen, en dan krijg ik dit. (Ik heb de werkelijke sterfte ook getekend. Stiekem heb ik ondertussen ook de bandbreedte uitgerekend, 2x de RMSE (root mean squared error), een maat voor hoe ver voorspellingen gemiddeld van de echte waarden afliggen. (RIVM spreekt van standaarddeviatie, waarschijnlijk om het voor de meeste mensen begrijpelijk te maken)

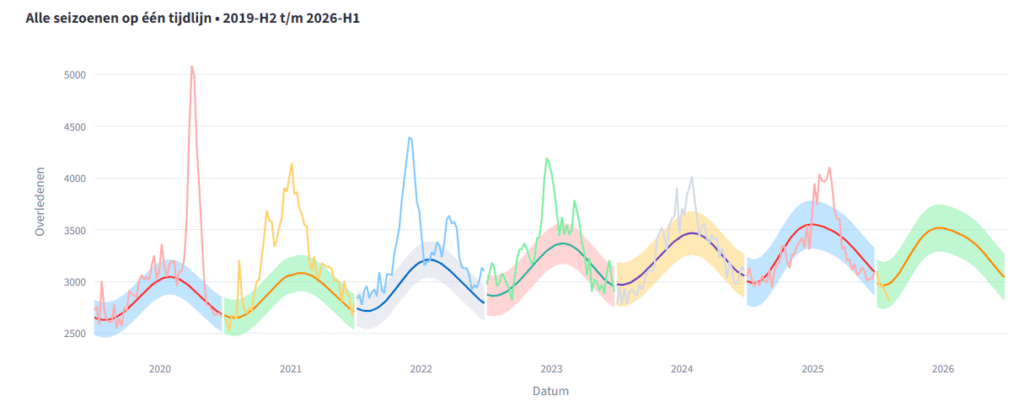
Waarom is 2026 nou lager?

Hiervoor leg ik de berekening voor doeljaren 2025 en 2026 over elkaar heen (plaatje door @infopinie die een betere versie heeft gemaakt dan ikzelf)

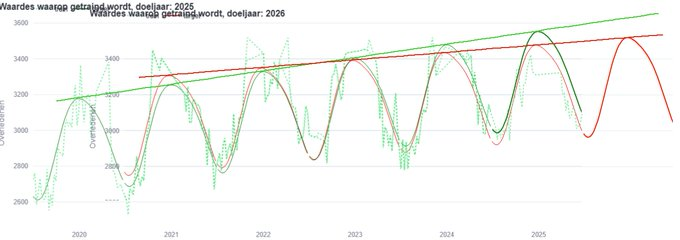
Je ziet dat die van 2025 (groen) sneller stijgt dan die van 2026 (rood) en daardoor hoger uitkomt. En waarom zijn die golven zoals ze zijn? Kwestie van het passend maken, zoals hierboven beschreven. De daling in de verwachte sterfte voor 2026 komt dus niet door een geheimzinnige agenda, maar door de manier waarop het algoritme de data selecteert en de waardes in de formule zo passend mogelijk maakt.

Het model vs de gepubliceerde cijfers

Tot slot worden de resultaten van mijn code met de gepubliceerde cijfers vergeleken

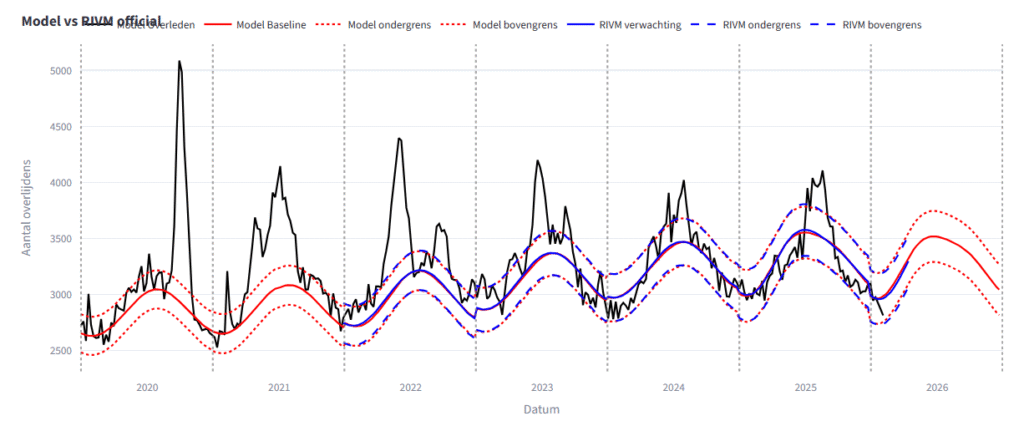
Als je het uitrekent in procenten, krijg je dit

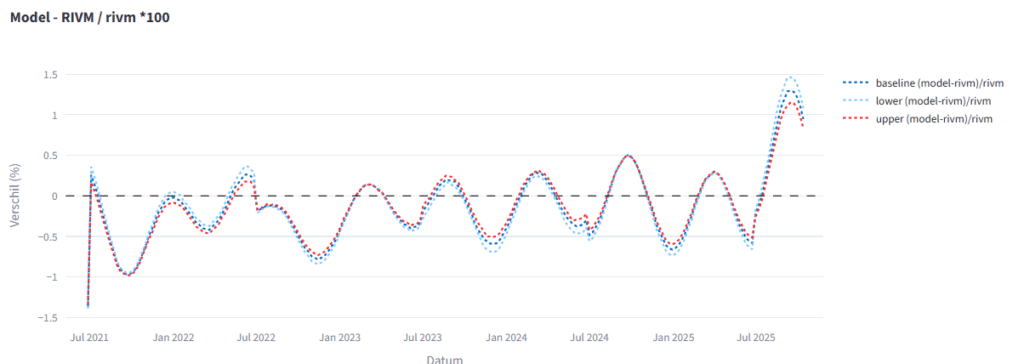
Waarom de afwijking in de laatste weken opeens relatief hoger is, is stof voor verder onderzoek, maar doet niets af aan het feit dat mijn code de methode van het RIVM goed benadert.

Slot

Wat uit deze beschrijving blijkt, is dat het RIVM-model geen magische black box is, maar zuivere wiskunde. Het gebruikt een vaste methode met een lineaire regressie die jaar op jaar op dezelfde manier wordt toegepast.

De opvallende daling in 2026 komt voort uit de manier waarop de regressie de golfbeweging fit en wiijst dus niet op een verborgen agenda. De vergelijking met de gepubliceerde cijfers laat zien dat de code de cijfers van het RIVM goed benadert. Het RIVM algoritme is transparant en de uitkomsten zijn verklaarbaar en te reproduceren.

Code : https://github.com/rcsmit/COVIDcases/blob/main/rivm_model.py

Interactieve versie : https://covid-menu-rcsmit.streamlit.app/?choice=61 (wake up when needed)

RIVM monitoring sterftecijfers: https://www.rivm.nl/monitoring-sterftecijfers-nederland