In the world of house cleaning, efficiency and thoroughness are key. But what happens when we apply data science and probability theory to this everyday task?
This summer I was preparing mobile homes on a camping. During this work, different thoughts and questions came up. How many days would I need to see at least all the houses at least once? How many days would I need to be for 95% sure that I have been in at least 95% of the accommodations? For reasons of readability I use the word cleaning instead of preparing/prepping. I assume that the houses are randomly assigned to me (in reality we get each day a number of houses which are close to each other)
For this I made a simulation. The simulation allows us to specify three key parameters:
- Number of days
- Total number of houses
- Houses cleaned per day
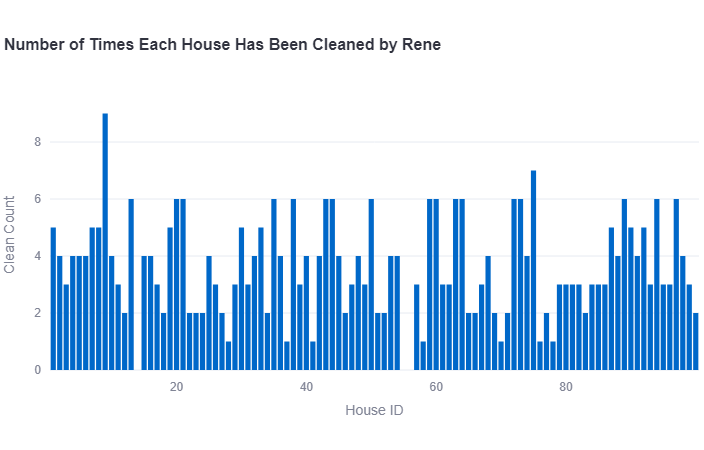
Simulation of Cleaning:
A part of the simulation runs through each day, randomly selecting houses for Rene to clean. This gives a realistic distribution of cleaning frequencies across all houses.
Probability of at least one house not being cleaned by Rene
The part calculates the probability that at least one house remains uncleaned after a given number of days. The formula used is:
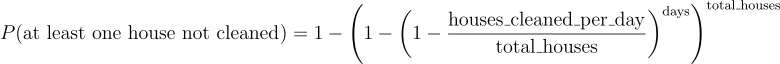
Let’s break it down step by step:
- Inner part: houses_cleaned_per_day / total_houses This represents the probability of a specific house being cleaned on any given day.
- 1 – (houses_cleaned_per_day / total_houses) This is the probability of a specific house NOT being cleaned on a given day.
- (1 – houses_cleaned_per_day / total_houses)^days This represents the probability of a specific house NOT being cleaned over the entire period of ‘days’.
- 1 – (1 – houses_cleaned_per_day / total_houses)^days This is the probability of a specific house being cleaned at least once during the period.
- (1 – (1 – houses_cleaned_per_day / total_houses)^days)^total_houses This represents the probability that ALL houses are cleaned at least once during the period.
- Finally, 1 – (1 – (1 – houses_cleaned_per_day / total_houses)^days)^total_houses This gives us the probability that at least one house is NOT cleaned during the entire period.
The formula uses the complement rule of probability. Instead of directly calculating the probability of at least one house not being cleaned (which would be complex), it calculates the probability of all houses being cleaned and subtracts that from 1.cularly useful because it allows us to calculate the probability of missing at least one house even when the number of houses and days is large, which would be computationally intensive to simulate directly.
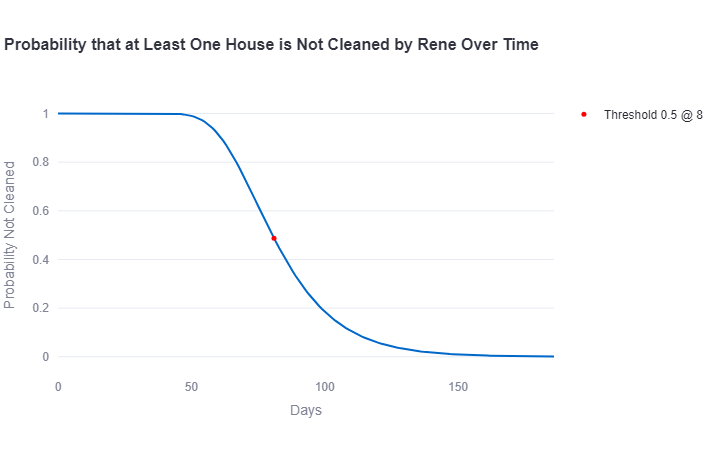
In the graph we can see that at the 81st day the chance that Rene has cleaned all the houses at least once is 50%.
The Challenge: Cleaning at Least 95% of Houses. How many days do I need
The script also calculates how many days it takes to reach a target probability that a certain percentage of houses have been cleaned at least once.
This challenge is modeled using probability theory, particularly the binomial distribution, which simulates the cleaning process. The idea is straightforward: each cleaning round has a certain probability of successfully cleaning each house. Over multiple rounds, we want to calculate how likely it is that a large percentage of houses—let’s say 95%—are cleaned at least once. But here’s the twist: we also want to be confident in this result, aiming for something like 95% certainty.
To do this, we turn to the binomial distribution. This distribution models the number of successes (in this case, houses cleaned) in a series of independent trials (cleaning rounds). For each trial (or cleaning attempt), there’s a probability of success (cleaning a house), and the goal is to determine how many rounds are needed to ensure at least 95% of the houses have been cleaned.
The goal isn’t just to clean a few houses during each round but to make sure that at least 95% of all the houses have been cleaned after multiple days. To calculate this, we use the cumulative probability—the likelihood that a certain percentage of houses are cleaned. This is where the binomial cumulative distribution function (CDF) comes in. The CDF calculates the probability that fewer than 95% of the houses are cleaned, and by subtracting this from 1, we find the probability of cleaning at least 95%.
Here’s the key concept:
- We compute the cumulative probability of cleaning fewer than 95% of the houses.
- Then, subtract this value from 1 to get the probability of cleaning at least 95%.
The formula looks like this:
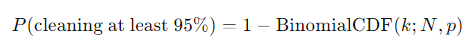
Where
k=⌊0.95×N⌋ represents 95% of the total number of houses (rounded down to the nearest whole number).
N is the total number of houses.
p is the probability that a house is cleaned in a single round.
BinomialCDF(k;N,p) gives the cumulative probability of cleaning fewer than k houses out of N, each with probability p.
So, the probability of cleaning at least 95% of the houses is calculated as 1 minus the probability of cleaning fewer than 95%.
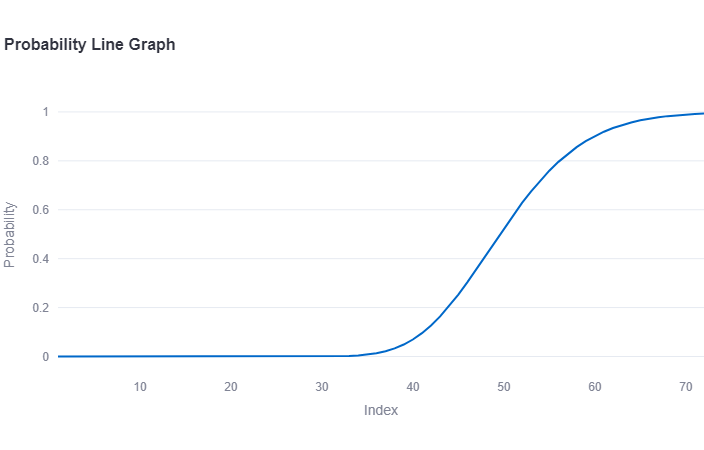
For example, suppose you have 100 houses to clean, and the probability of cleaning any given house on a single day is the same for all houses. If you want to ensure with 95% confidence that at least 95% of the houses have been cleaned at least once, and you can clean 6 houses per day, you would need around 64 days to reach that target.
This method allows us to predict the required number of cleaning rounds to meet both the coverage goal (cleaning 95% of the houses) and the confidence level (95% certainty), providing a clear path to optimizing the cleaning schedule.
Practical Applications:
While our example focuses on house cleaning, this model could be adapted to various scenarios requiring systematic coverage of multiple units over time, such as:
- Maintenance schedules for a fleet of vehicles
- Quality control inspections in a large warehouse
- Rotating crop plantings across multiple fields
By adjusting the parameters and running multiple simulations, we can optimize schedules and resource allocation for many real-world scenarios.
Final thoughts
This simulation demonstrates how applying statistical methods to everyday tasks can provide valuable insights and improve efficiency. It’s a prime example of how data science can transform even the most mundane activities into opportunities for optimization and understanding.
Simulation coded with assistence of ChatGPT. The article is written with the help of AI (ClaudeAI / ChatGPT)
