Understanding Temporal Variability in Bus Arrival Times and Its Implications on Travel Planning
Introduction
Efficient public transportation is vital for urban areas, offering convenience and reducing environmental impact. However, unpredictable bus schedules pose challenges for commuters, making it difficult to arrive on time for appointments or connections. This study focuses on two bus lines that are supposed to run regularly but often deviate from their schedules due to traffic congestion and other operational factors.
Hypothesis
The hypothesis tested in this study is rooted in a practical joke often relayed to travelers at the information point: advising passengers to leave earlier than scheduled to ensure punctuality due to perceived bus schedule unpredictability. The bus drive took 40 minutes.
The hypothesis suggests leaving:
- One hour early: Provides a 70% probability of arriving on time. (taken in account 20 minutes wait)
- Ninety minutes early: Increases the probability to 95%. (taken in account 45 minutes wait)
- Two hours early: Ensures near certainty (99.5%) of on-time arrival.(taken a margin of 80 minutes)
Methodology
To test this hypothesis, the study employs empirical data collection and statistical analysis:
- Data Collection: Recording actual bus arrival times, noting deviations from the published schedule.
- Statistical Analysis: Applying the Exponential distribution to model the probability of buses arriving within specified time intervals, accounting for average arrival rates and variability.
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time if these events occur with a known constant mean rate and independently of the time since the last event.(*)
Under a Poisson distribution with the expectation of λ events in a given interval, the probability of k events in the same interval is
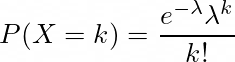
Exponential Distribution
The exponential distribution is the probability distribution of the distance between events (in this case the time between two busses) in a Poisson point process.
The probability density function is
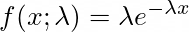
The cumulative distribution function is given by
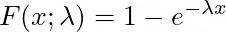
If we apply this to our problem, the formula is
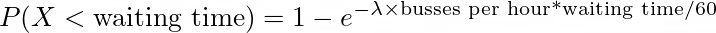
We divide the waiting time in minutes by 60 to get the waiting time per hour (because the number of busses is also per hour)
Assumptions
For these distributions, the events have to be independent and occur at a constant mean rate. While this assumption may not be entirely accurate in reality, we proceed with it for the purposes of our analysis.
Results
The waiting times have been noted during the summer of 2016 (n=47) and have been organized into intervals. A frequency table has been created, and the cumulative frequencies have been calculated. (read the waiting times as <=1, <=5, <=60 >60
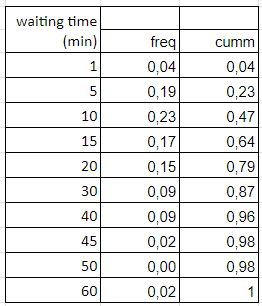
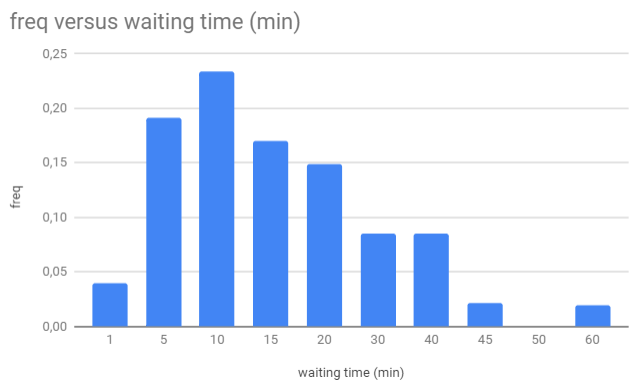
The waiting times have been plotted in a cumulative distribution chart
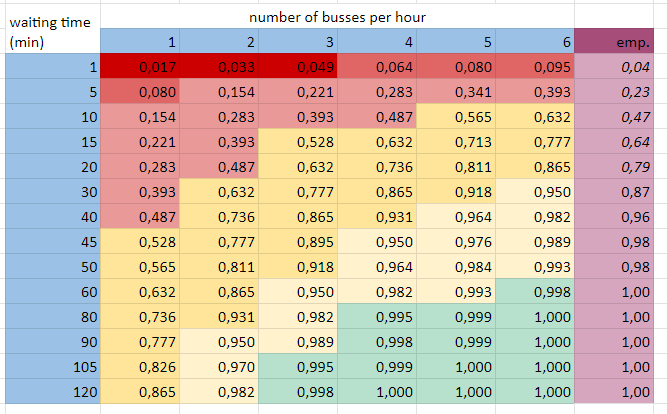
We compared these theoretical cumulative probabilities of the possible number of busses per hours with empirical data collected from actual waiting times.

This has been plotted in a graph.
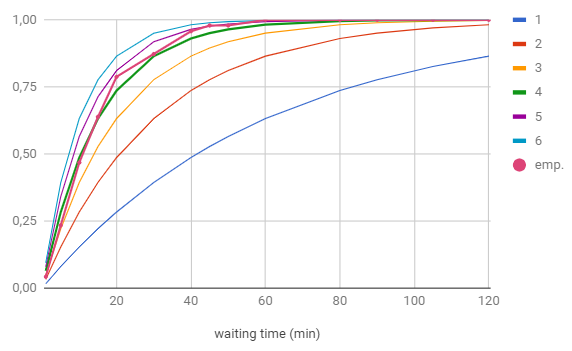
Comparing the empirical values with the cumulative distribution we can assume that there are approximately 4 à 5 busses passing by per hour.
To be on the safe side, we assume for our advice that k = 4. This is fitting the fact that there were two bus lines with each two busses per hour at the time.
Conclusion
We consider that the bus ride takes approximately 40 minutes. Based on this, we can conclude:
- There is a 74% probability of arriving on time if one leaves one hour early.
- This probability increases to 96% when departing 90 minutes ahead.
- Leaving two hours early ensures near certainty (99.5%) of arriving on time.
These probabilities align closely with the initial joke and hypothesis of the study.
The research validates this hypothesis through rigorous empirical evidence and statistical modeling.
Discussion
While this study provides valuable insights into the temporal variability of bus arrival times and its implications for travel planning, several limitations and areas for further investigation deserve attention.
Simplifying Assumptions:
The assumption of independent and constant-rate bus arrivals, essential for the Poisson and Exponential distributions used in this study, simplifies the analysis but may not fully capture the complex realities of urban transportation dynamics. Factors such as traffic congestion, weather conditions, and operational delays can significantly impact bus schedules, introducing variability that these models may not fully account for. Future research could explore more sophisticated modeling approaches that integrate real-time data and dynamic factors to better reflect the stochastic nature of bus arrivals.
Limited Scope and Data:
This study focused on a specific timeframe (summer 2016) and a small sample size (n=47) of waiting times from only two bus lines. These waiting times have been mostly in the afternoon. While it provides valuable insights into these specific contexts, the findings may not generalize to other timeframes, seasons, locations, or bus routes with different operational characteristics. Increasing the scope of data collection across various conditions and routes would enhance the robustness and applicability of the conclusions.
Model Applicability:
While the Poisson and Exponential distributions are commonly used in probability theory and statistics, their application to bus arrival times assumes a level of regularity that may not always hold true in practice. Variations in passenger demand throughout the day, changes in bus schedules, and unforeseen disruptions challenge the strict adherence to these distributions. Future studies could explore alternative modeling techniques or adaptations that better accommodate the dynamic nature of urban transit systems.
Future Directions:
This study suggests future research could benefit from incorporating real-time data analytics and passenger perceptions to refine models and improve public transportation reliability further. By integrating these insights, policymakers and transit operators could develop more responsive scheduling strategies that account for both operational realities and commuter expectations.
References
- https://en.wikipedia.org/wiki/Poisson_distribution
- https://en.wikipedia.org/wiki/Exponential_distribution
