In een artikel van Marc Jacobs over oversterfte wordt een aanname van het CBS.
De aanname is dat elke graad Celsius dat deze temperatuur hoger is dan de gemiddelde temperatuur in de week 3 tot en met 10 leidt tot 1 procent minder sterfte. Wanneer de temperatuur boven de 16,5 graad stijgt, neemt de sterfte weer toe met 2 procent per graad
Ik besloot dit te fact checken
Methode
Ik heb de KNMI weerggevevens opgehaald van locatie De Bilt van 2000 tot en met 2019. Hierdoor zijn de COVID-jaren buiten beschouwing genomen.[*]
De gemiddelde weektemperatuur is genomen. (dit is het gemiddelde de gemiddelde dagtemperatuur van 7 dagen)
Ik heb de wekelijkse sterftegegevens opgehaald vanaf Eurostats [*]
Met behulp van Python, plotly en Streamlit zijn deze verwerkt en weergegeven.
Als we de sterfte afzetten tegen de temperatuur zien we een mooie curve.
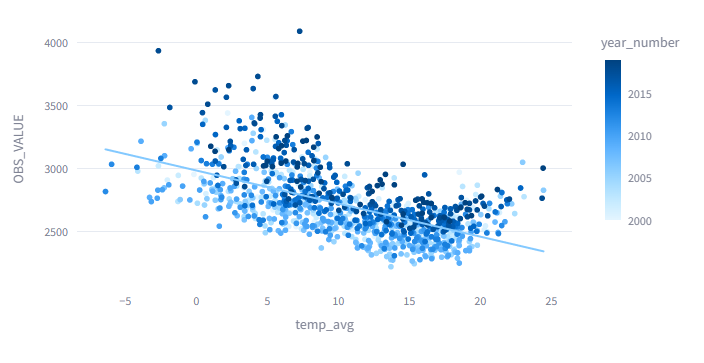
We hebben de curve opgesplitst in 2 gedeeltes, onder de 16,5 graad en boven de 16,5 graad
Onder de 16,5
We hebben het aantal overlijdens uitgezet tegenover de gemiddelde temperatuur als deze onder de 16,5 was
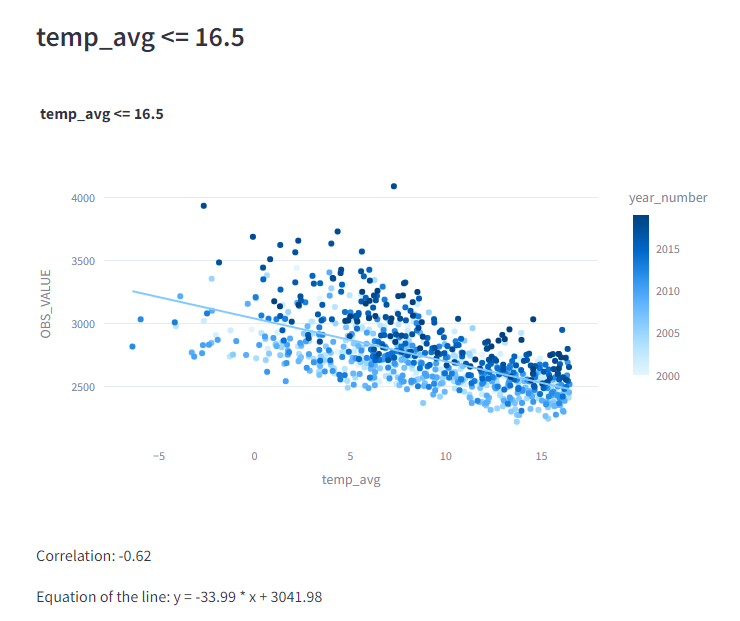
We hebben de gemiddelde sterfte genomen van alle weken tussen week 3 tot en met en 10 (te weten 3055 personen) en dit op 100 gesteld.
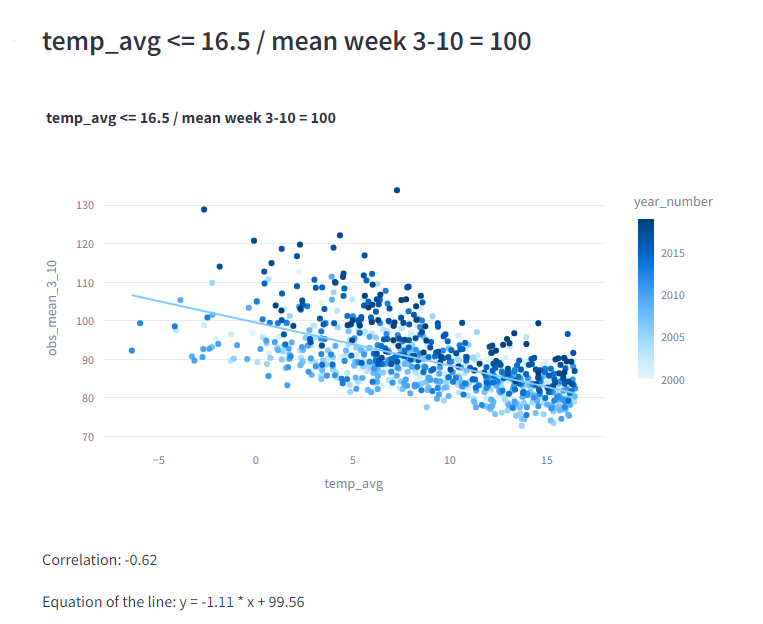
We krijgen dus een trendlijn met de formule y=-1.11x + 99.56
We hebben ook de gemiddelde temperatuur tussen week 3 en 10 berekend (te weten 10,85 graad) en de daarbijbehorende verwachte sterfte genomen vanuit grafiek 2 (3042) en deze op 100 gesteld
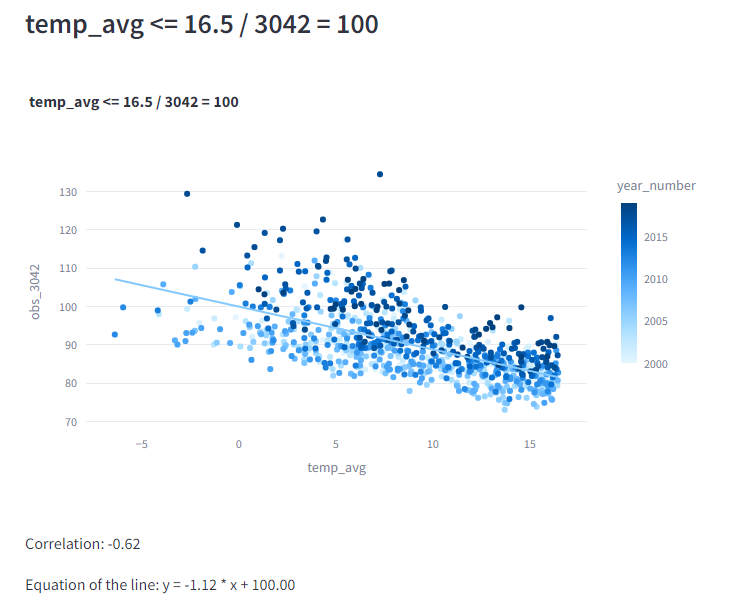
Ook deze heeft een trendlijn waarvan de coeffcient rond de 1 graad ligt
Boven de 16,5
Tevens hebben een grafiek gemaakt waarbij de waarde van de trendlijn op 16,5 (te weten 2461) op 100 is gesteld

De formule van deze trendlijn is y=1,97x+67,17
Poisson regressie analyse
Er is ook een Poisson regression analyses uitgevoerd. Deze regressie analyse wordt uitgevoerd indien er sprake is van aantallen zoals in dit geval.
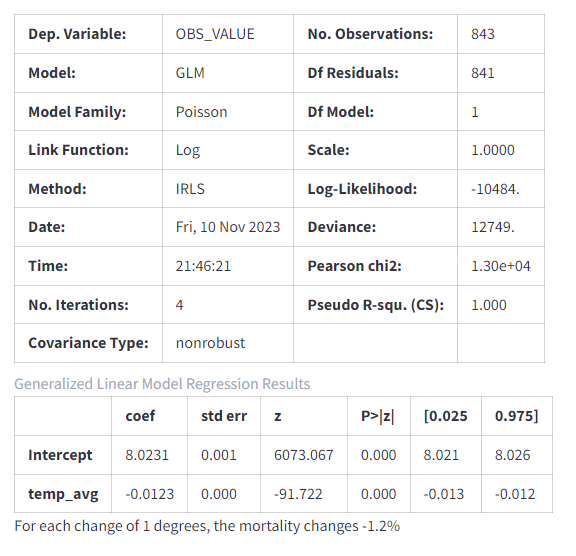

Ook hier komen de -1% en 2% weer terug.
Conclusie
Uit dit zeer eenvoudig exploratieve onderzoekje kunnen we concluderen dat de aanname van het CBS juist lijkt te zijn
Discussie
Commentaar van Marc Jacobs:
Je laat niet zien dat de aanname van het CBS juist is, je laat zien waarschijnlijk hoe het CBS erbij gekomen is. Autocorrelatie met een regressie analyseren is statistisch incorrect. Dat is hoe je komt op een waarde die biologisch niet kan
(opmerking van de auteur: alle onderzoeken in de links hieronder gebruiken een vorm van regressie)
Er is vast ook een mogelijkheid waarbij je de (gemiddelde) seizoenstrend als 1 variable neemt en de temperatuur als een andere afhankelijke variabele en daardoor de invloed van de temperatuur kan bepalen.
De trendlijn onder de 16,5 graad lijkt geen rechte lijn te zijn
Er is maar een periode van 20 jaar gekozen. Dit zou herhaald moeten worden met een grotere periode.
Er wordt geen rekening gehouden met veranderende bevolking en/of verwachte levensverwachting etc.
Er wordt geen rekening gehouden met een vertraging. In Gasparini (2015) wordt een vertraging van 21 dagen genoemd.
Links
[1] Interactieve versie :https://rcsmit.streamlit.app/?choice=31
[2] Broncode: https://github.com/rcsmit/streamlit_scripts/blob/main/sterfte_temperatuur.py
[3] Sterftedata: https://raw.githubusercontent.com/rcsmit/streamlit_scripts/main/input/sterfte_eurostats_weekly__2000_01__2023_41.csv vanaf https://ec.europa.eu/eurostat/databrowser/bookmark/fbd80cd8-7b96-4ad9-98be-1358dd80f191?lang=en
[4] Weerdata: https://www.daggegevens.knmi.nl/klimatologie/daggegevens?stns=260&vars=TEMP:SQ:SP:Q:DR:RH:UN:UX&start=20000101&end=20231110
Bronnen / meer info
Bao, 2016. The influence of temperature on mortality and its Lag effect: a study in four Chinese cities with different latitudes [uses Poisson regression model combined with a distributed lag nonlinear model]
Folkerts, 2022. Sex differences in temperature-related all-cause mortality in the Netherlands [gebruikt Distributed lag non-linear models (DLNM) van Gasparini]
Garssen, 2005. The effect of the summer 2003 heat wave on mortality in the Netherlands [gebruikt linear regression]
Gasparini, 2015. Mortality risk attributable to high and low ambient temperature: a multicountry observational study [gebruikt distributed lag non-linear model]
Hoek, 2004. Weather and mortality in the Netherlands [gebruikt Poisson regression analysis]
Huynen, 2001. The Impact of Heat Waves and Cold Spells on Mortality Rates in the Dutch Population [gebruikt Poisson loglinear regression analyses]
