It sounds like something pulled from science fiction or a poetic metaphor: every time you breathe, you might be inhaling a molecule from Julius Caesar’s final exhale. But this idea is more than just a thought experiment — it’s grounded in probability, physics, and some surprisingly simple math.
Let’s walk through how this works, why the logic holds up (mostly), and how a small Python script can reveal something profound about the connectedness of our world.
The Basic Idea
When Caesar died in 44 BC, his final breath released trillions of molecules into the air. Over time, these molecules dispersed into the Earth’s atmosphere. Today, thanks to natural processes like diffusion, wind patterns, and the constant exchange of air, those same molecules are still around — albeit scattered.
Now think about your own breath. Each time you inhale, you’re taking in approximately 10²² molecules. With enough mixing and enough time, it’s statistically plausible — even likely — that a few of those molecules came from Caesar.
But how can we actually calculate that probability?
Modeling It with Binomial Probability
The core of the math comes from the binomial distribution — a statistical tool used when you repeat the same experiment multiple times and each repetition (or “trial”) has only two outcomes: success or failure.
In our case:
- Each molecule you inhale is a “trial”.
- A molecule is either from Caesar’s breath (success) or not (failure).
- The total number of molecules you inhale is the number of trials.
- The probability that any one molecule is from Caesar is incredibly small, but not zero.
What we want to know is: What’s the probability that at least one of these molecules is from Caesar’s breath?
That’s written mathematically as: P(X>0)=1−P(X=0)P(X > 0) = 1 – P(X = 0)
where X is the number of “successes” (molecules from Caesar’s breath) in n trials (molecules you inhale), each with probability p.
If that probability is high — say, over 99,9% — then we can confidently say that, yes, you are inhaling part of Caesar’s last breath.
A More Tangible Example: Pee in the Ocean
To make things more concrete, let’s switch examples.
Suppose someone pees 300 milliliters into the ocean. After a long time, the molecules from that pee become fully mixed into all of Earth’s water. You then drink a 250 ml glass of seawater. What are the odds that it contains even one molecule from the original urine?
We calculate:
- Molecules in 300 ml of urine ≈ 1.01 × 10²⁵
- Molecules in all the oceans ≈ 4.47 × 10⁴⁷
So the probability that any one molecule in your glass is from that pee is:
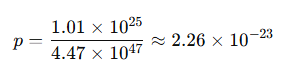
But you’re not drinking just one molecule. A 250 ml glass contains around 8.36 × 10²⁴ molecules.
If the molecules are perfectly mixed, the probability that your air contains at least one molecule from the original air is virtually 100%.
Even though the chance for one molecule is tiny, you try so many times that the odds stack up fast.
But Do Molecules Mix That Well?
This is where real-world physics enters the picture.
The binomial model assumes:
- All molecules are evenly mixed
- Every molecule acts independently
- The chance of success stays the same each time
That’s not completely true. Molecules don’t mix instantly. In fact, mixing in the ocean can take decades or centuries, especially in deep water. In the atmosphere, mixing happens faster — on the scale of months or years — but still not immediately.
To account for this, we added a mixing efficiency factor to our code. It’s a number between 0 and 1:
- 1 means perfect mixing
- 0 means no mixing at all
- Values in between represent partial mixing
Instead of blindly using p = n / m, we now calculate:
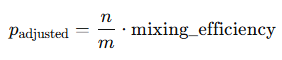
Then we recalculate the probabilities.
What the Graph Shows
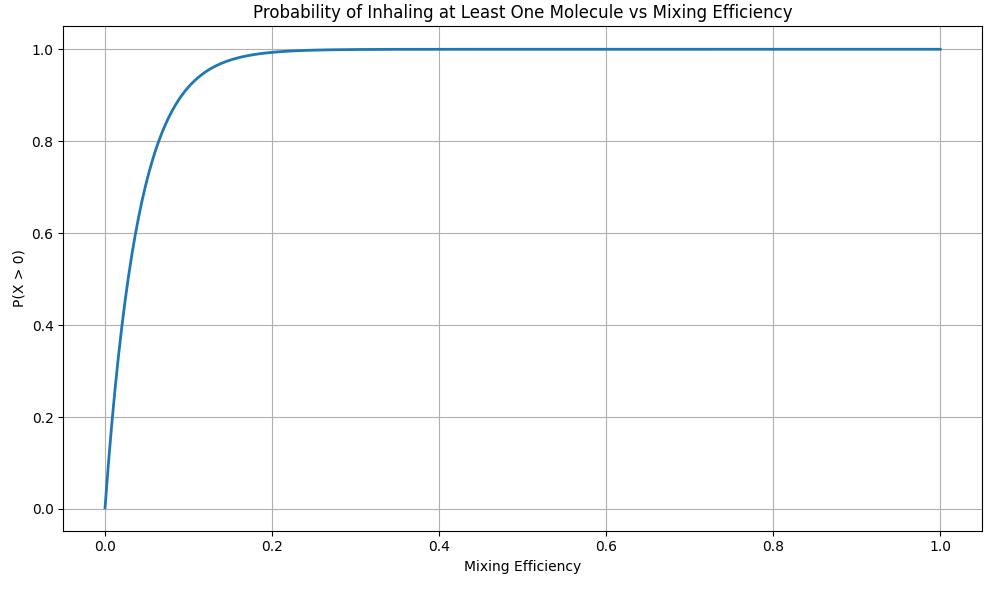
We graphed the chance of swallowing at least one molecule or air against the mixing efficiency, and the results were surprising:
- With only 18,4% mixing efficiency, the chance of getting a molecule from the original air of Caesar is already over 99%.
- Molecules moving around
- Probability doing its thing
- A bit of time
In other words:
You don’t need perfect mixing. You only need a small amount of diffusion for the math to tip in favor of “yes, you probably inhaled one”.
The same logic applies to the air you breathe. After a few years, the Earth’s atmosphere is mixed well enough that the chances of inhaling a molecule from Caesar’s final breath are extremely high.
The Bigger Picture
What starts as a quirky trivia question — “Could I breathe in Caesar’s last breath?” — actually becomes a fascinating lesson in how the world works at the molecular level.
This is not magic or mysticism. It’s just:
The takeaway isn’t just about Caesar or pee. It’s about how everything on Earth is part of a shared system — not just metaphorically, but physically. The world is more connected — chemically and physically — than most people realize. The air you breathe and the water you drink are ancient, recycled, and thoroughly global.
renesmit